Skewness is a measure of the asymmetry of a probability distribution. In a perfectly symmetrical distribution (like the Normal distribution), the left and right sides are mirror images of each other. However, real-world data is often “skewed” toward one side.
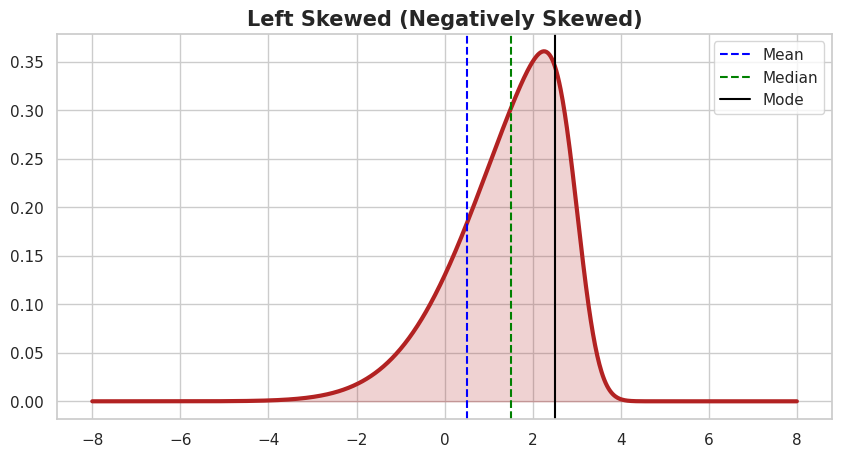
1. Left-Skewed (Negatively Skewed)
A distribution is left-skewed if it has a long “tail” that extends toward the left side.
- Property: The mean is typically pulled to the left by the low-value outliers.
- Relationship: Mean < Median < Mode.
- Real-world Example: Test scores. Test scores often show a left-skewed distribution, with most students scoring well and a few scoring far below average.
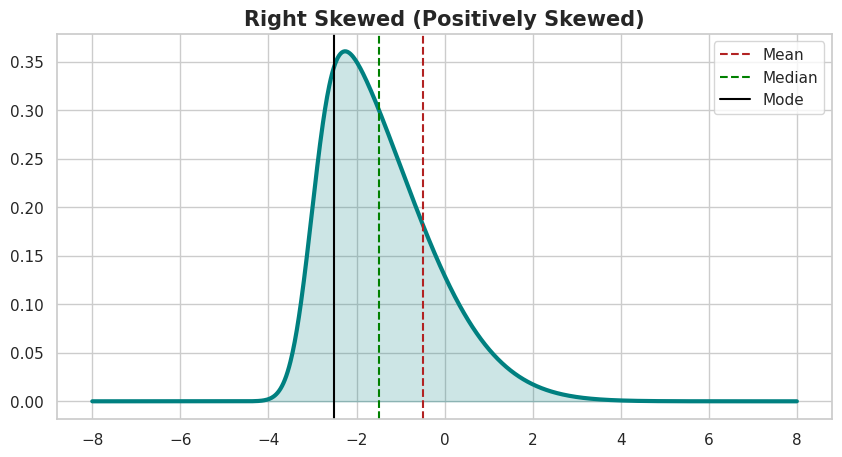
2. Right-Skewed (Positively Skewed)
A distribution is right-skewed if it has a long “tail” that extends toward the right side.
- Property: The mean is typically pulled to the right by the high-value outliers.
- Relationship: Mode < Median <Mean
- Real-world Example: House prices in a city: Many homes are moderately priced, with a few very expensive luxury properties.
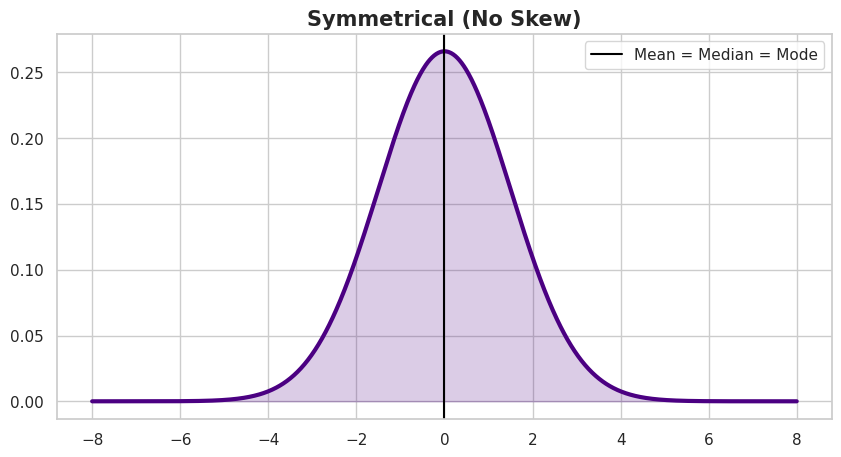
3. Symmetrical (Zero Skew)
A distribution has no skew if it is symmetrical on both sides.
- Property: The data is distributed evenly around the center.
- Relationship: Mean = Median = Mode.
- Real-world Example: Adult Heights. Adult heights in a large population tend to follow a symmetrical distribution, with most individuals clustered around the average and fewer individuals at equally distant values above and below it.