How to Interpret Type 1, Type 2, and Type 3 ANOVA

1. Introduction

What are the meanings of different types of ANOVA? In other words, what are Type 1 (Type I), Type 2 (Type II), and Type 3 (Type III) ANOVA? The following uses the model of factors A and B, and its interaction A*B as an example to explain the difference of Type 1 (Type I), Type 2 (Type II), and Type 3 (Type III) ANOVA.

2. Type 1 ANOVA (Type I ANOVA)

2.1 Definition of Type 1 ANOVA

SS(A) for factor A
SS(B | A) for factor B
SS(AB | A, B) for interaction AB

The following includes the explanations for each statement in Type 1 ANOVA.

SS(A) is SS attributable to A, even including those that could also have been attributed to other factors like B or A*B. Thus, SS(A) is equal to the model of only putting A as the single predictor.
SS(B | A) = SS (A, B) – SS(A)
SS(AB|A,B) = SS (AB, A, B) – SS(A, B)

2.2 Other Attributes

Type 1 ANOVA is sequential sum of squares, since it considers the order of entering factors into the model. The order of you write factors A and B in the model impacts the SS calculated for the factors.
If you add all different components of SS and do some simple math, you will get the following.

SS_A + SS_{B | A} +SS_{AB | A, B} + SSE = SST

3. Type 2 ANOVA (Type II ANOVA)

3.1 Definition of Type 2 ANOVA

SS(A | B) for factor A
SS(B | A) for factor B
SS(AB | A, B) for interaction AB

The following includes the explanations for each statement in Type 2 ANOVA.

SS(A|B) = SS (A, B) – SS(B)
SS(B|A) = SS (A, B) – SS(A)
SS(AB|A,B) = SS (AB, A, B) – SS(A, B).

3.2 Other Attributes and Comments

SS(A|B) and SS(B|A) do not control the impact of AB. Thus, if the interaction AB is significant, you need to be cautious interpretating SS(A | B) and SS(B | A).
When AB is insignificant, it seems to me that you do not really have to add AB into the model either, unless you really have a good reason.
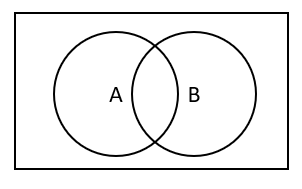
Type 2 ANOVA does not include the shared SS between A and B (i.e., the shared area of A and B circles, see below). At first, it is a bit counter-intuitive, as you would kind of guess that SS(AB | A, B) should be from the shared area of A and B circles. However, SS(AB | A, B) means that it excludes SS from the combination of A and B. Thus, SS(AB | A, B) is SS totally outside of A and B, and at the same time attributable to AB. That is, the shared SS of A and B (i.e., the overlap in two circles) is NOT part of SS(AB | A, B) at all. (For more, see a discussion on Stackexchange.)

Note that, SS_AB|A,B and SSE are the same as the counterparts in Type I ANOVA.
We can do some simple manth as follows. If A and B have no overlap, namely SS(A,B) =SS(A)+SS(B), we can get SS_A|B+SS_B|A+SS_AB|A,B+SSE = SST. However, if there is overlap (i.e., there is shared area between A and B circles), SS_A|B+SS_B|A+SS_AB|A,B+SSE ≠ SST

SS_A|B+SS_B|A+SS_AB|A,B

=SS(A,B)-SS(B)+SS(A,B)-SS(A)+SS(AB,A,B)-SS(A, B)

=SS(AB,A,B)+SS(A,B)-SS(A)-SS(B)

4. Type 3 ANOVA (Type III ANOVA)

4.1 Definition of Type 3 ANOVA

SS(A | B, AB) for factor A
SS(B | A, AB) for factor B
SS(AB | A, B) for interaction AB

The following includes the explanations for each statement in Type 3 ANOVA.

SS(A|B,AB) = SS (AB, A, B) – SS(AB, B)
SS(B|A,AB)= SS (AB, A, B) – SS(AB, A)
SS(AB|A,B)= SS (AB, A, B) – SS(A, B)

4.2 Other Attributes and Comments

SS that could be attributed to 2 or more combination (e.g., B and AB, A and AB, A and B) are not used.
I agree with the post on R-bloggers that, when the interaction AB is significant, you need to use Type 3 ANOVA. Further, when the interaction effect is significant, typically you need to focus on the simple main effects, rather than the main effects of A | B, AB or B | A, AB, which are difficult to explain, in my opinions.
When the interaction AB is not significant, you can just drop the AB in the model, unless you have a good reason to keep it. If you drop AB in the model, Type 2 and Type 3 ANOVA are the same.
When using Type 3 ANOVA (or even Type 1 and 2), it is better to specify which type of ANOVA you are using when reporting the results. Then, readers can make their judgment.
If A and B are not related (orthogonal), we can get SS_A|B,AB+SS_B|A,AB+SS_AB|A,B+SSE=SST. Otherwise, we likely to get SS_A|B,AB+SS_B|A,AB+SS_AB|A,B+SSE≠SST.