F-Distribution Critical Value Table
The following is the F Distribution Critical Value Table. The numbers in the table are critical values for F distribution with probably p in right tail of the distribution (see the figure illustration below).
F Distribution Critical Values
| df2 | p-value | df1 (Degrees of freedom in numerator) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 12 | 24 | 1000 | ||
| 1 | 0.05 | 161.4 | 199.5 | 215.7 | 224.6 | 230.2 | 234.0 | 236.8 | 238.9 | 243.9 | 249.1 | 254.2 |
| 0.025 | 647.8 | 799.5 | 864.2 | 899.6 | 921.8 | 937.1 | 948.2 | 956.6 | 976.7 | 997.3 | 1017.8 | |
| 0.01 | 4052 | 4999 | 5404 | 5624 | 5764 | 5859 | 5928 | 5981 | 6107 | 6234 | 6363 | |
| 2 | 0.05 | 18.51 | 19.00 | 19.16 | 19.25 | 19.30 | 19.33 | 19.35 | 19.37 | 19.41 | 19.45 | 19.49 |
| 0.025 | 38.51 | 39.00 | 39.17 | 39.25 | 39.30 | 39.33 | 39.36 | 39.37 | 39.41 | 39.46 | 39.50 | |
| 0.01 | 98.50 | 99.00 | 99.16 | 99.25 | 99.30 | 99.33 | 99.36 | 99.38 | 99.42 | 99.46 | 99.50 | |
| 3 | 0.05 | 10.13 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.89 | 8.85 | 8.74 | 8.64 | 8.53 |
| 0.025 | 17.44 | 16.04 | 15.44 | 15.10 | 14.88 | 14.73 | 14.62 | 14.54 | 14.34 | 14.12 | 13.91 | |
| 0.01 | 34.12 | 30.82 | 29.46 | 28.71 | 28.24 | 27.91 | 27.67 | 27.49 | 27.05 | 26.60 | 26.14 | |
| 4 | 0.05 | 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 | 5.91 | 5.77 | 5.63 |
| 0.025 | 12.22 | 10.65 | 9.98 | 9.60 | 9.36 | 9.20 | 9.07 | 8.98 | 8.75 | 8.51 | 8.26 | |
| 0.01 | 21.20 | 18.00 | 16.69 | 15.98 | 15.52 | 15.21 | 14.98 | 14.80 | 14.37 | 13.93 | 13.47 | |
| 5 | 0.05 | 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4.82 | 4.68 | 4.53 | 4.37 |
| 0.025 | 10.01 | 8.43 | 7.76 | 7.39 | 7.15 | 6.98 | 6.85 | 6.76 | 6.52 | 6.28 | 6.02 | |
| 0.01 | 16.26 | 13.27 | 12.06 | 11.39 | 10.97 | 10.67 | 10.46 | 10.29 | 9.89 | 9.47 | 9.03 | |
| 6 | 0.05 | 5.99 | 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 | 4.00 | 3.84 | 3.67 |
| 0.025 | 8.81 | 7.26 | 6.60 | 6.23 | 5.99 | 5.82 | 5.70 | 5.60 | 5.37 | 5.12 | 4.86 | |
| 0.01 | 13.75 | 10.92 | 9.78 | 9.15 | 8.75 | 8.47 | 8.26 | 8.10 | 7.72 | 7.31 | 6.89 | |
| 7 | 0.05 | 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 | 3.57 | 3.41 | 3.23 |
| 0.025 | 8.07 | 6.54 | 5.89 | 5.52 | 5.29 | 5.12 | 4.99 | 4.90 | 4.67 | 4.41 | 4.15 | |
| 0.01 | 12.25 | 9.55 | 8.45 | 7.85 | 7.46 | 7.19 | 6.99 | 6.84 | 6.47 | 6.07 | 5.66 | |
| 8 | 0.05 | 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 | 3.28 | 3.12 | 2.93 |
| 0.025 | 7.57 | 6.06 | 5.42 | 5.05 | 4.82 | 4.65 | 4.53 | 4.43 | 4.20 | 3.95 | 3.68 | |
| 0.01 | 11.26 | 8.65 | 7.59 | 7.01 | 6.63 | 6.37 | 6.18 | 6.03 | 5.67 | 5.28 | 4.87 | |
| 9 | 0.05 | 5.12 | 4.26 | 3.86 | 3.63 | 3.48 | 3.37 | 3.29 | 3.23 | 3.07 | 2.90 | 2.71 |
| 0.025 | 7.21 | 5.71 | 5.08 | 4.72 | 4.48 | 4.32 | 4.20 | 4.10 | 3.87 | 3.61 | 3.34 | |
| 0.01 | 10.56 | 8.02 | 6.99 | 6.42 | 6.06 | 5.80 | 5.61 | 5.47 | 5.11 | 4.73 | 4.32 | |
| 10 | 0.05 | 4.96 | 4.10 | 3.71 | 3.48 | 3.33 | 3.22 | 3.14 | 3.07 | 2.91 | 2.74 | 2.54 |
| 0.025 | 6.94 | 5.46 | 4.83 | 4.47 | 4.24 | 4.07 | 3.95 | 3.85 | 3.62 | 3.37 | 3.09 | |
| 0.01 | 10.04 | 7.56 | 6.55 | 5.99 | 5.64 | 5.39 | 5.20 | 5.06 | 4.71 | 4.33 | 3.92 | |
| 12 | 0.05 | 4.75 | 3.89 | 3.49 | 3.26 | 3.11 | 3.00 | 2.91 | 2.85 | 2.69 | 2.51 | 2.30 |
| 0.025 | 6.55 | 5.10 | 4.47 | 4.12 | 3.89 | 3.73 | 3.61 | 3.51 | 3.28 | 3.02 | 2.73 | |
| 0.01 | 9.33 | 6.93 | 5.95 | 5.41 | 5.06 | 4.82 | 4.64 | 4.50 | 4.16 | 3.78 | 3.37 | |
| 14 | 0.05 | 4.60 | 3.74 | 3.34 | 3.11 | 2.96 | 2.85 | 2.76 | 2.70 | 2.53 | 2.35 | 2.14 |
| 0.025 | 6.30 | 4.86 | 4.24 | 3.89 | 3.66 | 3.50 | 3.38 | 3.29 | 3.05 | 2.79 | 2.50 | |
| 0.01 | 8.86 | 6.51 | 5.56 | 5.04 | 4.69 | 4.46 | 4.28 | 4.14 | 3.80 | 3.43 | 3.02 | |
| 16 | 0.05 | 4.49 | 3.63 | 3.24 | 3.01 | 2.85 | 2.74 | 2.66 | 2.59 | 2.42 | 2.24 | 2.02 |
| 0.025 | 6.12 | 4.69 | 4.08 | 3.73 | 3.50 | 3.34 | 3.22 | 3.12 | 2.89 | 2.63 | 2.32 | |
| 0.01 | 8.53 | 6.23 | 5.29 | 4.77 | 4.44 | 4.20 | 4.03 | 3.89 | 3.55 | 3.18 | 2.76 | |
| 18 | 0.05 | 4.41 | 3.55 | 3.16 | 2.93 | 2.77 | 2.66 | 2.58 | 2.51 | 2.34 | 2.15 | 1.92 |
| 0.025 | 5.98 | 4.56 | 3.95 | 3.61 | 3.38 | 3.22 | 3.10 | 3.01 | 2.77 | 2.50 | 2.20 | |
| 0.01 | 8.29 | 6.01 | 5.09 | 4.58 | 4.25 | 4.01 | 3.84 | 3.71 | 3.37 | 3.00 | 2.58 | |
| 20 | 0.05 | 4.35 | 3.49 | 3.10 | 2.87 | 2.71 | 2.60 | 2.51 | 2.45 | 2.28 | 2.08 | 1.85 |
| 0.025 | 5.87 | 4.46 | 3.86 | 3.51 | 3.29 | 3.13 | 3.01 | 2.91 | 2.68 | 2.41 | 2.09 | |
| 0.01 | 8.10 | 5.85 | 4.94 | 4.43 | 4.10 | 3.87 | 3.70 | 3.56 | 3.23 | 2.86 | 2.43 | |
| 30 | 0.05 | 4.17 | 3.32 | 2.92 | 2.69 | 2.53 | 2.42 | 2.33 | 2.27 | 2.09 | 1.89 | 1.63 |
| 0.025 | 5.57 | 4.18 | 3.59 | 3.25 | 3.03 | 2.87 | 2.75 | 2.65 | 2.41 | 2.14 | 1.80 | |
| 0.01 | 7.56 | 5.39 | 4.51 | 4.02 | 3.70 | 3.47 | 3.30 | 3.17 | 2.84 | 2.47 | 2.02 | |
| 50 | 0.05 | 4.03 | 3.18 | 2.79 | 2.56 | 2.40 | 2.29 | 2.20 | 2.13 | 1.95 | 1.74 | 1.45 |
| 0.025 | 5.34 | 3.97 | 3.39 | 3.05 | 2.83 | 2.67 | 2.55 | 2.46 | 2.22 | 1.93 | 1.56 | |
| 0.01 | 7.17 | 5.06 | 4.20 | 3.72 | 3.41 | 3.19 | 3.02 | 2.89 | 2.56 | 2.18 | 1.70 | |
| 100 | 0.05 | 3.94 | 3.09 | 2.70 | 2.46 | 2.31 | 2.19 | 2.10 | 2.03 | 1.85 | 1.63 | 1.30 |
| 0.025 | 5.18 | 3.83 | 3.25 | 2.92 | 2.70 | 2.54 | 2.42 | 2.32 | 2.08 | 1.78 | 1.36 | |
| 0.01 | 6.90 | 4.82 | 3.98 | 3.51 | 3.21 | 2.99 | 2.82 | 2.69 | 2.37 | 1.98 | 1.45 | |
| 1000 | 0.05 | 3.85 | 3.00 | 2.61 | 2.38 | 2.22 | 2.11 | 2.02 | 1.95 | 1.76 | 1.53 | 1.11 |
| 0.025 | 5.04 | 3.70 | 3.13 | 2.80 | 2.58 | 2.42 | 2.30 | 2.20 | 1.96 | 1.65 | 1.13 | |
| 0.01 | 6.66 | 4.63 | 3.80 | 3.34 | 3.04 | 2.82 | 2.66 | 2.53 | 2.20 | 1.81 | 1.16 | |
- How can I find the critical f-value?
You need to know the alpha level (e.g., α = 0.05, i.e., p-value = 0.05), degree of freedom in numerator, namely df1 (e.g., df1 = 5), and degree of freedom in denominator, namely df 2 (e.g., df2 = 20). By having these 3 numbers, you will find the critical value of 2.71 from the table.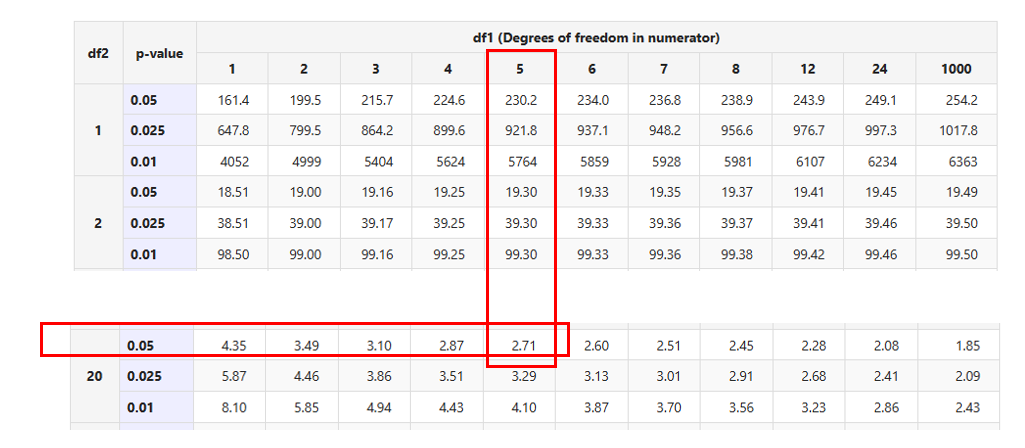
- How can I decide alpha level (p-value)?
Typically, people will go by alpha = 0.05 (i.e., p-value = 0.05), if you do not have strong reasons for other alpha levels. Thus, you typically just need to focus on the rows of p-value = 0.05. - How can I know df1 (i.e., degree of freedom in numerator)?
This is based on your research designs and analyses. Let’s just use a simple example. If you are doing one-way ANOVA, and you have 3 groups, then df1 = 3-1 = 2. df1 (numerator) is the number of groups minus 1 for one-way ANOVA. - How can I know df2 (i.e., degree of freedom in denominator)?
Again, this is based on your research designs and analyses. For one-way ANOVA, you will use the formula of N-k. N is the total number of observations across all groups, whereas k is the number of groups (or levels of the factor being tested). For instance, if you have 90 participants from all 3 groups (e.g., each group has 30 participants, and thus 90 participants in total), df2 = 90 – 3 = 87. You might have quesition that there is no df2= 87 on the table. Note that, this is a static table, and the space limit makes it impossible to present all the possible combinations of df1 and df2. For the combination of df1 and df2 that you can not find from the table, you might want to consider using F-distribution calculator (Click Here) instead of this static table. - What can I do with the critical f-value?
After getting a critical f-value (e.g., 2.71), if the f-value you calculateed is great than 2.71, you will reject the null hypothesis. For one-way ANOVA, null hypothesis typicall states that there is no significant difference between groups on the dependent measure. - What do alpha (significance level) and critical f-value mean visually?
Below is the F-distribution density function illustration figure for the case of f(5, 20) = 2.71 and α (significance level) = 0.05. The α value corresponds to the shaded area under the curve (the red area). The critical f-value of 2.71 is the number on the x-axis, a cut-off point.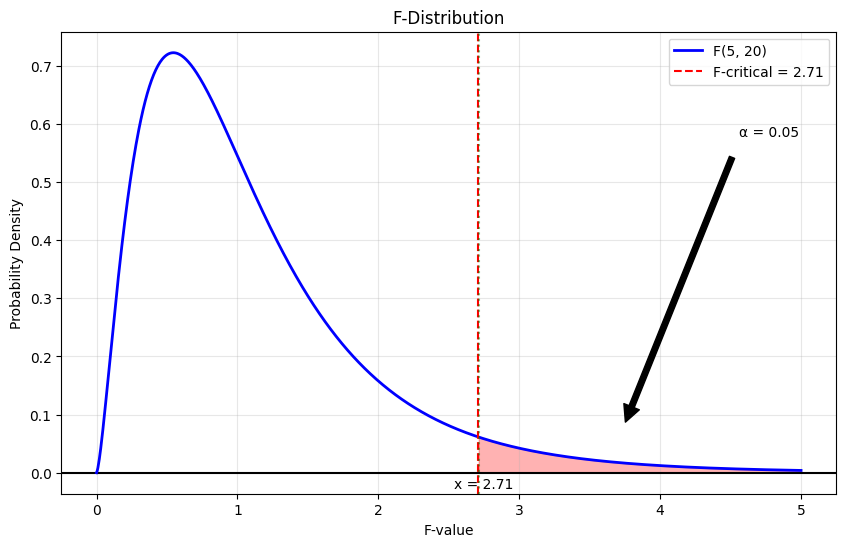
Discussion