The tutorial provides examples for each of these 4 normal distribution functions in R. R has 4 normal distribution functions, including rnorm, dnorm, pnorm, and qnorm.
The following table provides a summary for each of these 4 normal distribution functions in R.
| Syntax of R functions | Definitions | Examples |
|---|---|---|
| rnorm(n, mean, sd) | Generate a sample of normal distribution | rnorm(50) returns a sample of 50 data points, with mean = 0 and sd = 1. |
| dnorm(x, mean, sd) | Return the density of probability at point of x | dnorm(2) returns 0.05, which is the density value at point of x=2. |
| pnorm(q, mean, sd) | Return the probabiliy p = CDF value from (-∞, q). | pnorm(2) returns probability p= 0.977. |
| qnorm(p, mean, sd) | Return the quantile value q, based on the probability value of p. | qnorm(0.977) returns the quantile value q= 2. |
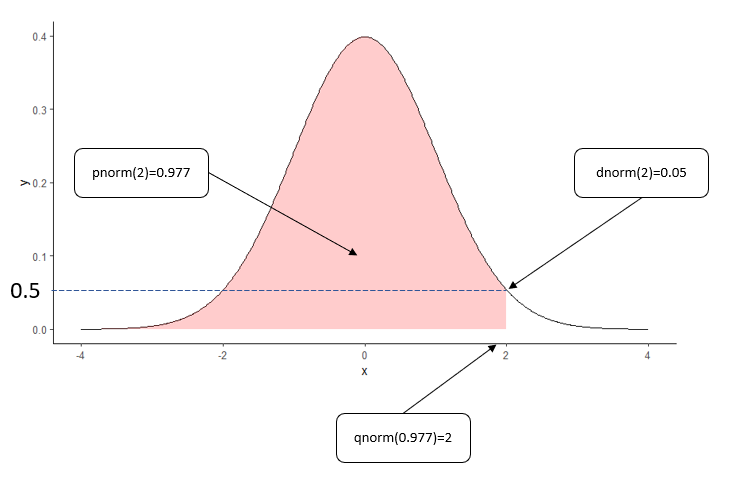
Examples of 4 normal distribution functions in R
Example 1: rnorm()
rnorm(50, 2, 4) will generate 50 data points with mean = 2 and sd =4.
The following is the R code of rnorm(50, 2, 4) and its output. It returns a sample of 50 data observations.
> rnorm(50, 2, 4) [1] -0.6595560 0.4281984 4.8785564 3.5895556 0.2748618 [6] 4.8687434 9.5170507 1.5709189 6.8071283 1.4665153 [11] 2.1283960 -3.8310225 1.4255138 -1.6046666 4.3547475 [16] 11.7897579 -1.4176837 8.3676064 5.1467558 0.8026364 [21] 10.6407257 3.0924876 0.5525197 1.4196198 2.7662511 [26] 0.2250933 -2.2283784 9.2073751 4.0276599 -0.6118463 [31] 2.3868138 3.0647955 0.6110670 4.9345245 0.9395610 [36] 2.2158906 4.0917283 4.0740428 -5.4952048 -1.5320750 [41] -0.5265014 -2.3662700 6.3202778 -0.9169152 -2.8141011 [46] 8.1260610 5.7547098 -1.2224999 1.7558709 5.6006177
Example 2: dnorm()
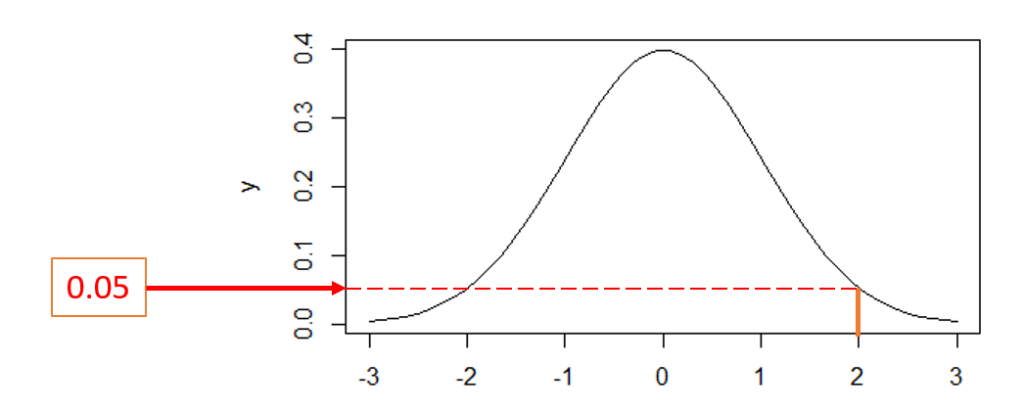
dnorm(2) returns the density of probability at x=2. Note that it is standard normal distribution with mean = 0 and SD = 1.
> dnorm(2) [1] 0.05399097
We can see that 0.054 is the density of probability at point of 2. Visually, it is the value on Y-axis in the bell shape curve of normal distribution (see the figure below).
Example 3: pnorm()
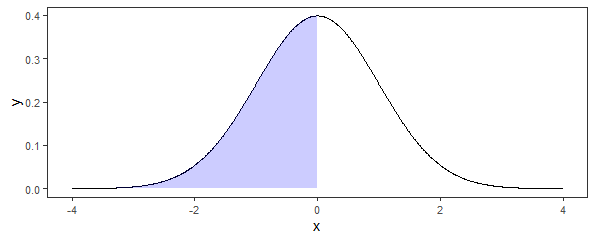
pnorm(0, 0, 1) returns 0.5, which is probability value of the CDF for the range of (-∞, 0) for standard normal distribution (i.e., mean = 0 and sd =1).
> pnorm(0, 0, 1) [1] 0.5
The following is the plot for pnorm(0, 0, 1). The area of the blue shade is 0.5.
Example 4: qnorm()
qnorm(0.5, 0, 1) returns 0, which is the quantile (i.e., value on the x-axis) for the probability of 0.5. As we can see, qnorm() is just the inverse side of pnorm().
> qnorm(0.5, 0, 1) [1] 0