Probability Density Function (PDF) provides the likelihood that the value of a random variable will fall between a certain range. PDF typically is used for continuous random variables. For discrete random variables, we use probability mass function.
Definition of Probability Density Function (PDF)
Probability Density Function (PDF) is defined as the probability of a value of the random variable in the span of Δx. Note that, Δx should be very small (close to zero).
\[ f_X(x)= \lim\limits_{\Delta x \rightarrow 0} \frac{Pr[x≤X≤x+\Delta x]}{\Delta x} \]
We do not say PDF returns the probability at point x is because the probability at any specific point for a continuous distribution will always be zero as the area under a point is 0.
That is, we connect PDF and probability via a very short range, namely Δx →0.
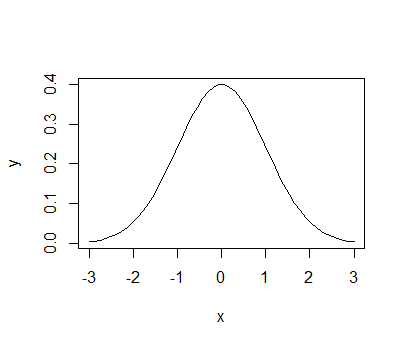
Example 1: PDF for Normal Distribution
The following is the PDF of normal distribution.
\[ f(x)=\frac{1}{\sqrt{2 \pi \sigma^2}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \]
If we use mean μ = 0 and standard deviation σ = 1, we can get the following PDF.
\[ f(x)=\frac{1}{\sqrt{2 \pi }}e^{-\frac{1}{2}x^2} \]
We can use R to plot this PDF. The following is the R code.
# generate a sequence of 50 numbers in the range of -3 and 3
x <- seq(-3, 3, length=50)
# use the normal distribution function dnorm() from R
y <- dnorm(x)
# plot x and y with a connected line
plot(x,y, type = "l")The following is the plot of the PDF of normal distribution in R.
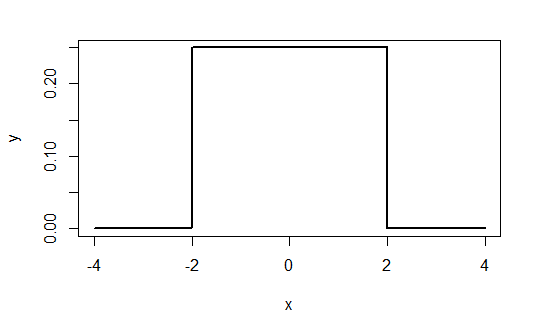
Example 2: PDF for Uniform Distribution
The following is PDF for uniform distribution.
\[ f(x) = \left\{ \begin{array}{rcl}
\frac{1}{b-a} & \mbox{for}
& a \le x \le b\\ 0 & \mbox{for} & x < a \ or \ x>b
\end{array}\right. \]
If we use a=-2, and b=2, we can get the following PDF.
\[ f(x) = \left\{ \begin{array}{rcl}
\frac{1}{4} & \mbox{for}
& -2 \le x \le 2 \\ 0 & \mbox{for} & x < -2 \ or \ x>2
\end{array}\right. \]
Similarly, we can use R to plot the uniform distribution PDF. Below is the R code.
# generate a range of data for x-axis
x <- seq(-4, 4, length=1200)
# calculate density for uniform distribution
y <- dunif(x, min = -2, max = 2)
# plot the uniform distribution
plot(x, y, type = 'l',lwd = 2)The following is the plot of the PDF of uniform distribution in R.
