Sample variance is the measure of the variability in a given sample. A sample is a set of observations that are a subset of a population.
Sample Variance Formula
The following is the formula for sample variance.
\[ s^2=\frac{\sum_{i=1}^n (x_i-\bar{x})^2}{n-1} \]
where,
- \( n \) is the number of observations in the sample.
- \( x_i \) is the ith observation.
- \(\bar{x} \) is the mean of the obervations.
Data Example
The following is a sample of 6 students with math scores.
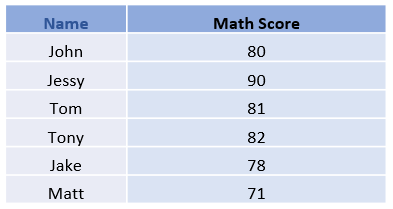
Calculating sample variance by hand
Step 1: the mean
The following calculates the mean of the sample. The numerator is the sum of all observations, and the denominator is the number of the sample.
\( \bar{x} = \frac{80+90+81+82+78+71}{6} = 80.33 \)
Step 2: sample variance
The following is to calculate the sample variance. Note that, the denominator is 6-1, rather than 6.
\( s^2=\frac{(80-80.33)^2+(90-80.33)^2+(81-80.33)^2+(82-80.33)^2+(78-80.33)^2+(71-80.33)^2}{6-1} = 37.87 \)
