This tutorial provides examples to explain vectors and arrows in space (vector visualization). It includes 2 and 3-dimension vectors as well as vector addition and subtraction.
Example 1: 2 dimension vectors
\( \vec{V_1} =(3, 2 ) = \left[\begin{array}{ccc}
3\\
2 \end{array}
\right]\)
Note that, \( (3, 2 ) \) and \( \left[\begin{array} {ccc} 3\\ 2 \end{array} \right]\) are equivalent. Further, \( \vec{V_1} \) can be visualized as follows (i.e., plotted on the \( \mathbb{R}^2 \) ).
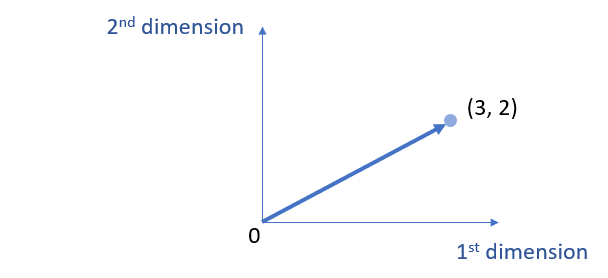
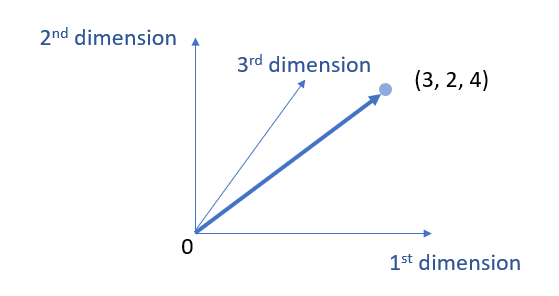
Example 2: 3 dimension vectors
Of course, vectors can have more than 2 dimensions, such as 3 dimensions, or even more.
\( \vec{V_1} =(3, 2, 4 ) = \left[\begin{array}{ccc}
3\\
2\\ 4 \end{array}
\right]\)
Example 3: Vector addition
The following is an example of vector addition and we use parallelogram law here.
\( \vec{Y}+\vec{X} = \left[\begin{array}{ccc} 1 \\ 3 \end{array} \right] + \left[\begin{array}{ccc} 3 \\ 2 \end{array} \right] =\left[\begin{array}{ccc} 4 \\ 5 \end{array} \right] \)
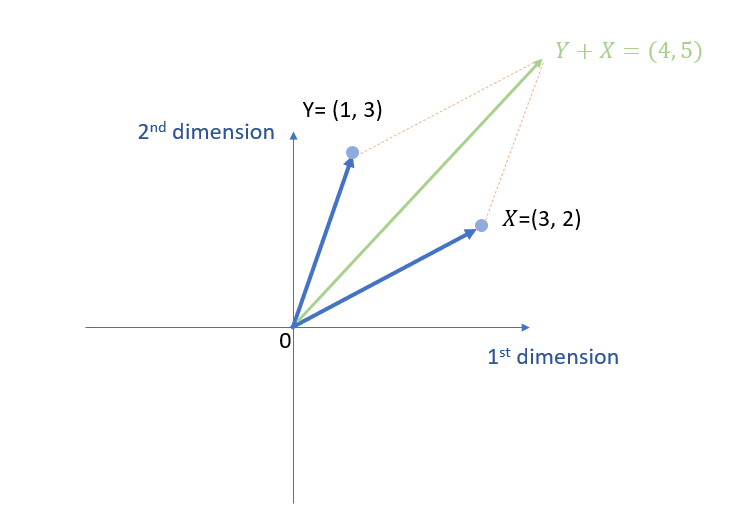
We can also use the triangle law for the addition of vectors. This method is also called the head-to-tail method. That is, two vectors can be added together by placing them together in such a way that the first vector’s head joins the tail of the second vector.
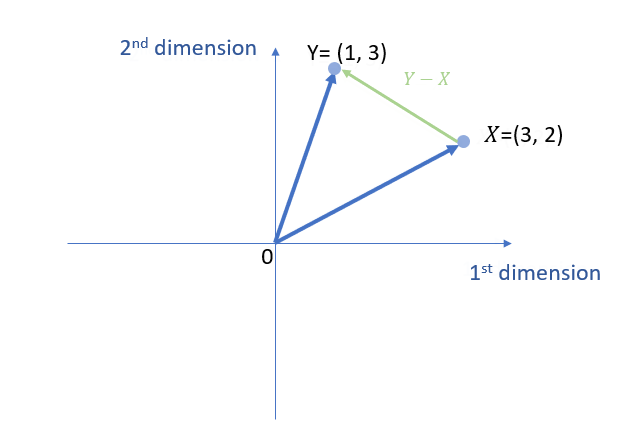
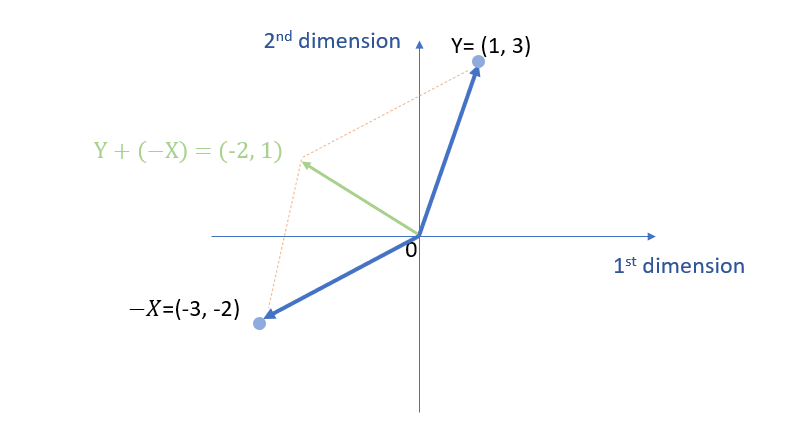
Example 4: Vector subtraction
The vector subtraction of two vectors a and b is represented by a – b. For this, we can use the triangle law.
\( \vec{Y}-\vec{X} = \left[\begin{array}{ccc} 1 \\ 3 \end{array} \right] – \left[\begin{array}{ccc} 3 \\ 2 \end{array} \right] \)
It can be also written as adding the negative of vector b to the vector a. i.e., a – b = a + (-b). With that, we can use the parallelogram law.
\( \vec{Y}-\vec{X} =\vec{Y}+\vec{-X}= \left[\begin{array}{ccc} 1 \\ 3 \end{array} \right] + \left[\begin{array}{ccc} -3 \\ -2 \end{array} \right] =\left[\begin{array}{ccc} -2 \\ 1 \end{array} \right] \)
Reference
Vector Intro for linear algebra (Khan Academy)