A linear subspace or vector subspace is a vector space that is a subset of some larger vector space.
To be considered a linear subspace, a vector set needs to meet the following 3 requirements.
- (1) The set includes the zero vector.
- (2) The set is closed (or, closure) under scalar multiplication.
- (3) The set is closed (or, closure) under addition.
For instance, if we say that \( V \) is a subset of \( \mathbb{R}^n \) and in order to make sure \( V \) is a subspace, it needs to meet the 3 requirements mentioned above.
First, it needs to include the n-dimension zero vector. For instance, if \( \mathbb{R}^n \) is \( \mathbb{R}^2 \), then \( V \) should include the 2 dimension 0 vector \( \vec{v} = \left[\begin{array}{ccc} 0 \\ 0 \end{array} \right]\).
Second, the set \( V \) is closed under scalar multiplication. This means that, for any in the vector set \( \vec{v} \), \( c\vec{v} \) must also be in \( V \), in which \( c\) is any real-number scalar.
Third, the set has to be closed under addition. This means that, if \( c_1 \vec{v_1} \) and \( c_2 \vec{v_2} \) are both vectors in the set \( V \), the vector \( c_1 \vec{v_1} + c_2 \vec{v_2} \) must also be in \( V \) as well. If you combine with the 2nd requirement, here, we are saying that any linear combination of the vectors in \( V \) will also be in \( V \).
Example 1
We can test if \( V_1 \) is a linear subspace.
\( V_1 = \{ \vec{v_1}=\left[\begin{array}{ccc} 0 \\ 0 \end{array} \right] \} \)
First, since it includes 0 vector \( \vec{v_1} \), it meets the first requirement. Second, any scalar \( c \), it will lead to a 0 vector. Third, since it is only one vector, it goes back to the second requirement.
Example 2
We can test if \( V_2 \) is a subspace.
\( V_2 = \{ \vec{v_1}=\left[\begin{array}{ccc} 0 \\ 0 \end{array} \right], \vec{v_2}=\left[\begin{array}{ccc} 2 \\ 3 \end{array} \right] \} \)
First, since it includes 0 vector \( \vec{v_1} \), it meets the first requirement. Second, if using the scalar 2 to time a vector \( 2\vec{v_2} = 2 \left[\begin{array}{ccc} 2 \\ 3 \end{array} \right] \), \( 2 \left[\begin{array}{ccc} 2 \\ 3 \end{array} \right] \) is not the set of \( V_2 \).
Example 3
Note that, a span is all of the linear combinations of the vector. We can also test if \( V_3 \), the span of a vector, is a linear subspace.
\( V_3 = span( \left[\begin{array}{ccc} 2 \\ 3 \end{array} \right]) \)
We can plot the line as follows, which goes through point (0, 0) and extends both sides.
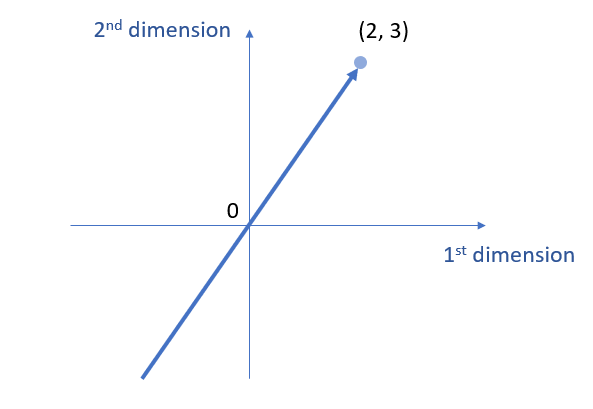
First, since it goes through \( \left[\begin{array}{ccc} 0 \\ 0 \end{array} \right] \), it meets the first requirement. Second, we time the vector using the scalar 2, namely \( 2\vec{v_2} = 2 \left[\begin{array}{ccc} 2 \\ 3 \end{array} \right] \), which is still on the span of the vector. Third, go back to requirement 2.
Reference
You can refer to the following two articles on linear subspaces.
Linear subspaces (Khan Academy)
Definition of A Linear Subspace
Further Reading
You can also read my other tutorials on the difference between Space and Subspace. Importantly, I also have tutorials on how to view mean as a projection and how to view linear regression as a projection as well.
