This tutorial explains the difference between space and subspace.
What is space?
The most simple example of space is the two-dimensional space, \( \mathbb{R}^2 \). You can visualize it as the xy-coordinate plane.
\( \mathbb{R}^2 \) is a vector space that contains all possible two-dimensional vectors \( \vec{v} = (x, y) \).
Similarly, \( \mathbb{R}^3 \) is a 3-dimensional vector space, which is also often known as the XYZ space.
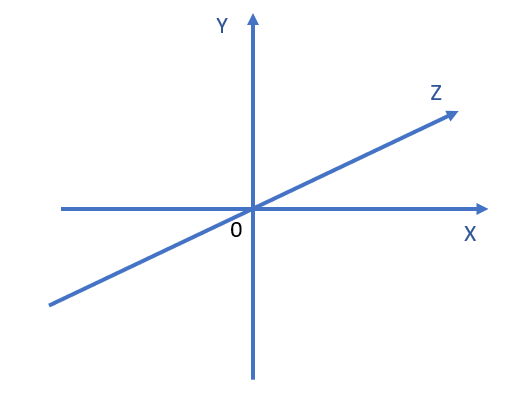
That is, \( \mathbb{R}^3 \) is the vector space that contains all possible three-dimensional vectors, \( \vec{v} = (x, y, z) \).
While it is difficult to visualize beyond 3 dimensions, there are 4 (\( \mathbb{R}^4 \)), 5 (\( \mathbb{R}^5 \)), or even higher dimension spaces.
Note that, you can see that the space discussed here is different from the vector arrow in space. In particular, a space emphasizes all the possible vectors with the same number of dimensions, regardless of 2, 3, or even higher dimensions.
In contrast, the visualization of vector arrow points in space is more to visualize where that vector is located and how it looks in the space (help humans to visually understand the concept of a vector).
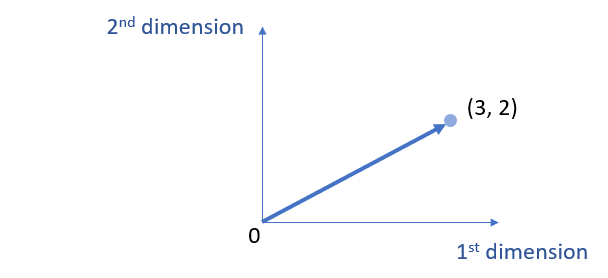
For instance, the following is to visualize the arrow of a vector but it does not specify a space. If anything, we can say that \( \vec{v_1} \) is a vector in the 2-dimensional vector space \( \mathbb{R}^2 \).
\( \vec{v_1} =(3, 2 ) = \left[\begin{array}{ccc}
3\\
2 \end{array}
\right]\)
What is subspace?
Given that a space includes all the possible vectors with the same dimension, there are subspaces (or, linear subspaces or vector subspaces) within a space.
For instance, a subspace of \( \mathbb{R}^2 \) is a set of two-dimensional vectors within \( \mathbb{R}^2 \). However, not any set of two-dimensional vectors can be considered as a subspace.
To be considered a linear subspace, a vector set needs to meet the following 3 requirements.
- (1) The set includes the zero vector.
- (2) The set is closed (or, closure) under scalar multiplication.
- (3) The set is closed (or, closure) under addition.
For instance, the vector set only including \( \vec{v_1} \) is not a subspace since it does not include a zero vector.
\( V = \{ \vec{v_1}=\left[\begin{array}{ccc} 3 \\ 2 \end{array} \right] \} \)
For more detailed examples and further explanations of subspace (click here), please refer to my other tutorial specifically on linear subspace.
