Population Variance Formula and Calculation by Hand
This tutorial shows the formula for population variance and the steps for calculating population variance by hand.
Formula
Population variance is the measure of the variability of a population. The following is the formula for population variance.
\[ \sigma^2=\frac{\sum_{i=1}^N (x_i-\mu)^2}{N} \]
where,
- \( N \) is the number of data points in the population.
- \( x_i \) is the ith data point.
- \(\mu \) is the mean of the population.
Population vs. Sample Data
The following is the population of a set of data. It has 11 observations, whereas the sample has 6. Typically, sample data is a subset of the population.
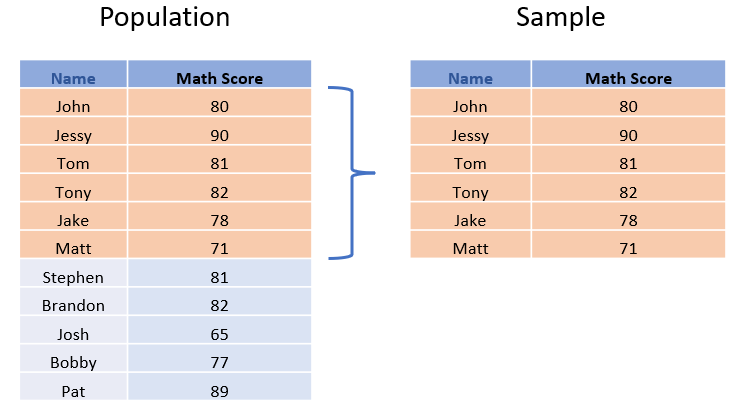
Calculating Population Variance
Step 1
The following is to calculate the population mean of \( \mu \), which is 79.64.
\(\mu = (80+90+81+…+77+89)/11=79.64 \)
Step 2
The following calculates the population variance.
\( \sigma^2=\frac{\sum_{i=1}^N (x_i-\mu)^2}{N} = \frac{(80-79.64)^2+(90-79.640^2+…+(89-79.64)^2}{11}=46.23 \)
Further Reading
It should be noted that the formulas for population variance and sample variance are different. The following is a tutorial is about sample variance.
Discussion