This tutorial shows the formula for population variance and the steps for calculating population variance by hand.
Formula
Population variance is the measure of the variability of a population. The following is the formula for population variance.
\[ \sigma^2=\frac{\sum_{i=1}^N (x_i-\mu)^2}{N} \]
where,
- \( N \) is the number of data points in the population.
- \( x_i \) is the ith data point.
- \(\mu \) is the mean of the population.
Population vs. Sample Data
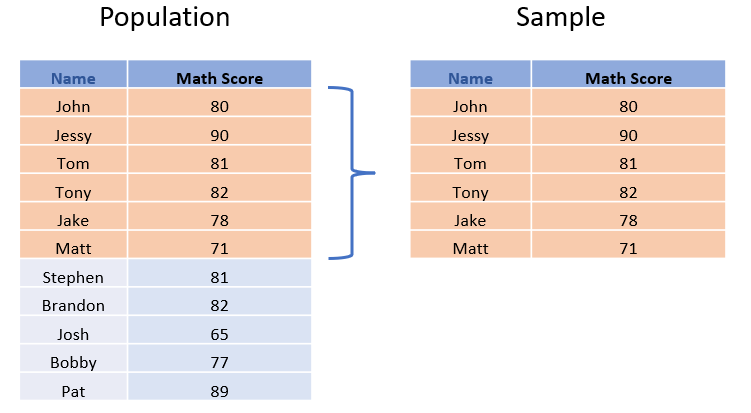
The following is the population of a set of data. It has 11 observations, whereas the sample has 6. Typically, sample data is a subset of the population.
Calculating Population Variance
Step 1
The following is to calculate the population mean of \( \mu \), which is 79.64.
\(\mu = (80+90+81+…+77+89)/11=79.64 \)
Step 2
The following calculates the population variance.
\( \sigma^2=\frac{\sum_{i=1}^N (x_i-\mu)^2}{N} = \frac{(80-79.64)^2+(90-79.640^2+…+(89-79.64)^2}{11}=46.23 \)
Further Reading
It should be noted that the formulas for population variance and sample variance are different. The following is a tutorial is about sample variance.
