Difference between ANOVA Two-Factor with Replication and without Replication

You use ANOVA: Two-Factor without Replication when each cell only has 1 observation, but use Two-Factor with Replication when each cell has more than 1 observation.

Options of ANOVA Two-Factor with Replication and without Replication in Excel
Options of ANOVA Two-Factor with Replication and without Replication in Excel

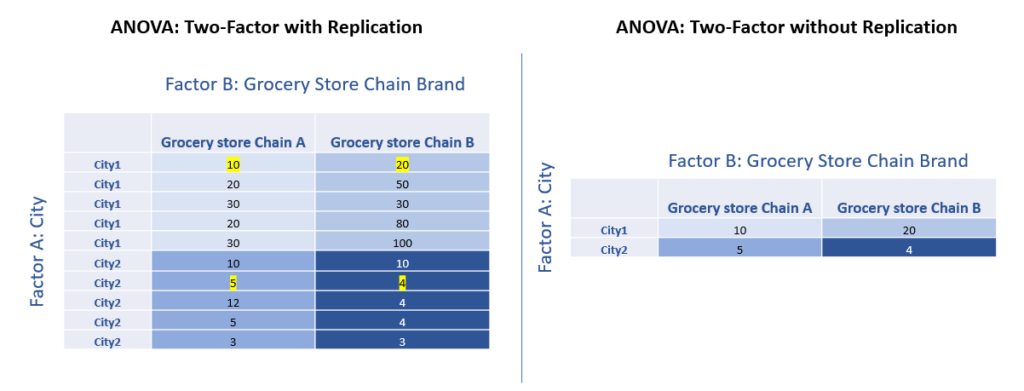
For instance, there are two factors, City and Chain Brand. Each has 2 levels, leading to 4 cells (see the figure below).

Each cell in the left-hand data table has 5 observations, and thus we use ANOVA: Two-Factor with Replication.

In contrast, each cell in the right-hand data table has only 1 observation, and thus we use ANOVA: Two-Factor without Replication.

Data Example for the difference between ANOVA Two-Factor with Replication and without Replication in Excel
Data Example for the difference between ANOVA Two-Factor with Replication and without Replication in Excel

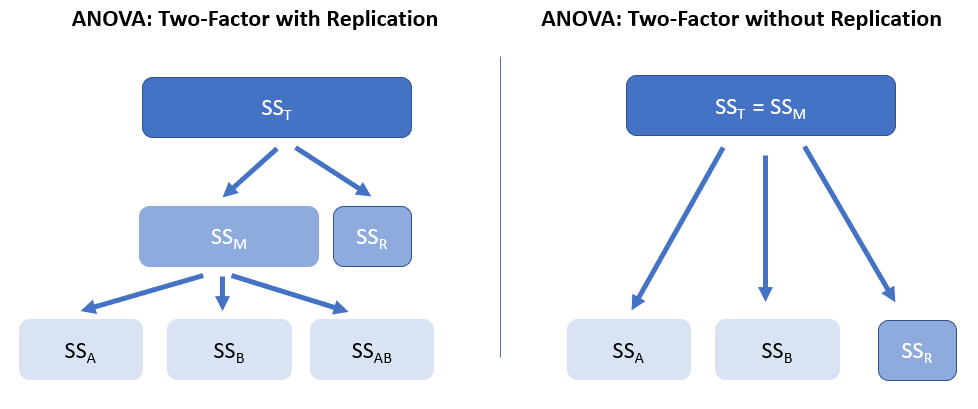
ANOVA Two-Factor with Replication and without Replication: Difference in Variance Partitioning

The following figure shows the difference in variance partitioning. In particular,

  • ANOVA with Replication: SST is divided into SSM and SSR, and there is an interaction term SSAB.
  • ANOVA without Replication: SST is equal to SSM, and there is no interaction term SSAB.
Variance partitioning for ANOVA Two-Factor with Replication and without Replication
Variance partitioning for ANOVA Two-Factor with Replication and without Replication

Reasons for No Interaction Term SSAB

There are two perspective to explain why there is no interaction term SSAB for ANOVA: Two-Factor Without Replication.

First, since each cell only one observation, \( x_{ij} \) is exactly the same as \( \bar{x_{ij}}\). Thus, you can not use the the same formula for SSR in two-factor ANOVA with replication. Instead, the formula for SSR for ANOVA two-Factor without Replication is as follows.

\( SS_R = \sum \sum (x_{ij}-\bar{x_i}-\bar{x_j}+\bar{x})^2 \)

where,

  • \( x_{ij} \) represents observation at \( i^{th} \) row and \( j^{th} \) column.
  • \( \bar{x_i}\) is the mean of observations for \( i^{th} \) row.
  • \( \bar{x_j}\) is the mean of observations for \( j^{th} \) row.
  • \( \bar{x}\) is the grand mean of all the cells.

Second, we can consider it from the degree of freedom perspective. The total degree of freedom is n-1 for SST. For instance, if you have 4 cells, dfT=3. Then, there is 1 df for SSA, and 1 df for SSB. Finally, there is only 1 df is left for SSR.

Further Reading

The following is the tutorial showing formulas for ANOVA Two-Factor without Replication and how to calculate it by hand and in Excel.

Further, there are related tutorials on this site on Two-factor ANOVA with replication.

Finally, there are two tutorials outside of this site as well.

Leave a Comment