How to Calculate Two-Factor ANOVA without Replication

ANOVA Two-Factor without Replication is used for a design of two factors (e.g., Factor A and Factor B) and only 1 observation in each cell.

For instance, both Factor A and Factor B have two levels, leading to 4 cells in total. Each cell only has 1 observations (see below).

---

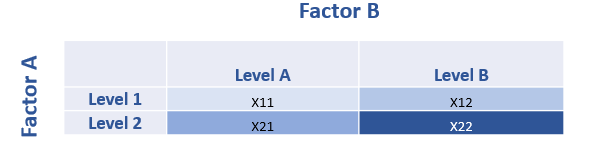
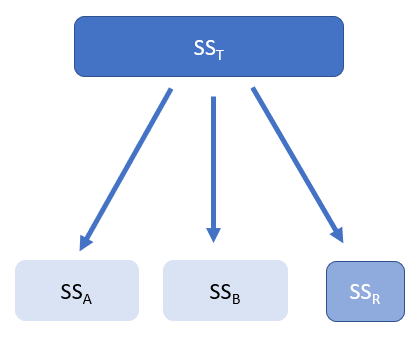
Variance Partitioning

Two-Factor ANOVA without Replication (SS_T) can be broken down into 3 part, SS_A, SS_B, and SS_R. The following is the figure showing the variance partitioning.

---

Formulas

The following shows the formulas for each components, including

\( SS_T=SS_A+SS_B+SS_R \)

For SS_T, you can use the following formula.

\( SS_T=\sum \sum (x_{ij}-\bar{x})^2 \)

where,

• \( i \) represents \( i^{th} \) row, \( j \) represents \( j^{th} \) column.
• \( x_{ij} \) represents observation at \( i^{th} \) row and \( j^{th} \) column.
• \( \bar{x}\) is the grand mean of all the cells.

For SS_A, the following is the formula.

\( SS_A= \sum n_i (\bar{x_i} -\bar{x})^2 \)

where,

• \( n_i \) represents the number of observations for \( i^{th} \) row.
• \( \bar{x_i}\) is the mean of observations for \( i^{th} \) row.
• \( \bar{x}\) is the grand mean of all the cells.

For SS_B, the following is the formula.

\( SS_B= \sum n_j (\bar{x_j} -\bar{x})^2 \)

where,

• \( n_j \) represents the number of observations for \( j^{th} \) column.
• \( \bar{x_j}\) is the mean of observations for \( j^{th} \) column.
• \( \bar{x}\) is the grand mean of all the cells.

The formula for SS_R is as follows.

\( SS_R = \sum \sum (x_{ij}-\bar{x_i}-\bar{x_j}+\bar{x})^2 \)

where,

• \( x_{ij} \) represents observation at \( i^{th} \) row and \( j^{th} \) column.
• \( \bar{x_i}\) is the mean of observations for \( i^{th} \) row.
• \( \bar{x_j}\) is the mean of observations for \( j^{th} \) row.
• \( \bar{x}\) is the grand mean of all the cells.

Note that, since \( x_{ij} \) is exactly the same as \( \bar{x_{ij}}\), you can not use the the same formula for SS_R in two-factor ANOVA with replication. Instead, SS_R here is the similar to interaction effect SS_AB in Two-Factor ANOVA with replication.

---

Calculate by Hand

The following is the data example used here.

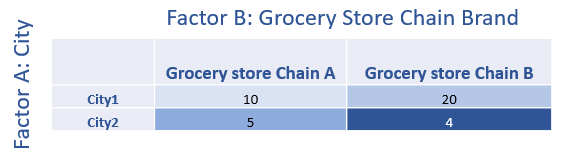
We can calculate the row and column means and grand mean as follow.

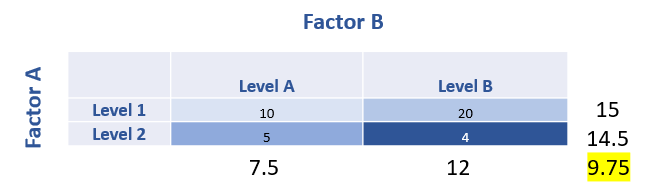
We can calculate SS_A, SS_B, and SS_R as follows.

SS_T= (10-9.75)² + (20-9.75)² +(5-9.75)² +(4-9.75)² =160.75

SS_A= 2(15-9.75)² + 2(14.5-9.75)² =110.25

SS_B= 2(7.5-9.75)² + 2(12-9.75)² =20.25

SS_R= (10-7.5-15+9.75)² + (20-12-15+9.75)² +(5-7.5-14.5+9.75)² +(4-12-14.5+9.75)² =30.25

Thus, we can see that SS_A+SS_B+SS_R =160.75 = SS_R.

We can calculate MS_A, MS_B, and MS_R as follows. Since all the degree of freedom is 1 for all of them. We can get the following.

MS_A= SS_A / df_A=110.25/1=110.25

MS_A =SS_B /df_B =20.25/1=20.25

MS_R = SS_R /df_R= 30.25/1=30.25

Finally, we can calculate the F-ratios as follows.

F_A=MS_A / MS_R =110.25/30.25=3.64

F_B=MS_B / MS_R =20.25/30.25=0.67

You can compare the output here with the output shown below using Excel. You can see that the results are the same.

---

Calculate using Excel

This section is to explain how to do ANOVA Two-Factor without Replication in Excel.

Step 1: Select menu options in Excel

You can select ANOVA: Two-Factor without Replication in Excel and click OK.

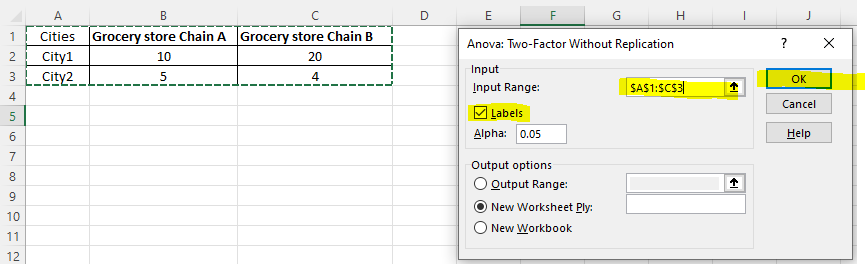
Step 2: Set data range in Excel

Then, you select A1 to C3 to the Input Range, click “Lables” and then “OK.”

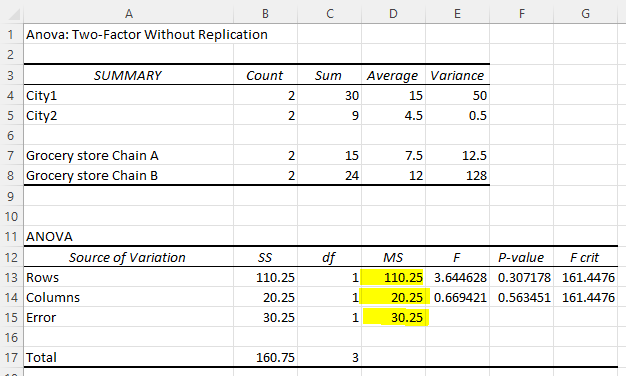
Step 3: Interpretation of the Excel output from two-factor ANOVA without Replication

The following are the null and alternative hypotheses for the effect of City.

• Null Hypothesis: City 1 and City 2 do not differ in sales.
• Alternative Hypothesis: City 1 and City 2 do differ in sales.

The following are the null and alternative hypotheses for the effect of Chain Brand.

• Null Hypothesis: Chain Brand A and Chain Brand B do not differ in sales.
• Alternative Hypothesis: Chain Brand A and Chain Brand B do differ in sales.

The following is the output from Excel. For the effect of City on sales, the p-value is greater than 0.05, and thus we fail to reject the null hypothesis. In other words, City 1 and City 2 do differ in sales.

For the effect of Chain Brand on sales, the p-value is greater than 0.05 and thus we fail to reject the null hypothesis. In other words, Chain Brand A and Chain Brand B do differ in sales.

---

Further Reading

There are tutorials on this site on Two-factor ANOVA with replication. You can check them out to have a better understanding on this topic.

• Two-Way ANOVA: Formula and Example (with replication)
• Two-Way ANOVA in Excel (with replication)

Finally, the following is a reference outside of this site.

• Two Factor ANOVA without Replication